Types Of Map Scales » Diagonal Scale, Plain Scale
Scale types – General Introduction And Definition The Scale Is The Device With The Help Of Which The Map Can Be Made By Giving The Whole Earth Or Any Part Of It, Small Or Big Size As Per The Requirement. That Is, The Scale Is The Ratio Between The Earth And The Map By Which The Actual Distance Between Any Two Points On The Night Can Be Represented By The Distance Between The Same Two Points On The Map.
Measurement –Distancebetween Two Pointsonthe Map / Distancebetween Thesame Two Points On The Ground
Fj Number.Ok House ( FJ Monk House As): ‘ Ruler That Is Between Those Two Points Between Any Two Points On The Articulated Connection Between The Map And The Ground. ”
Robinson , Randall And Morrison ( Robinson , Randall And Morrison According To): – The ‘Relationship Found Between Reality And Representation Is The Ruler. “
Methods To Scale Have ( Methods Of Expressing The Scale )
There Are Three Methods Of Displaying A Scale On A Map .
1. Simple Statement Method
2. Representative Fraction Method
3. Linear Scale Method
(1) Simple Statement Method ( Simple Statement Method )
By This Method, The Description Of The Scale Of A Map Is Given By Literal Interpretation. That Is, The Scale Is Written In Words On The Map. Like 1 Inch: 1 Mile Or 1 Cm. : 1 Km. Etcetera. This Is The Simplest Method Of Expressing A Scale. Often Land Asset Maps Display The Scale By This Method. But The Use Of This Method Is Quite Limited. Because One, Only Those People Who Are Familiar With The Measurement System Can Understand This Measurement Method. And On Changing The Size Of The Second Map, The Scale Becomes Impure.
(2) Appraiser Different Method ( Representative Fraction (RE) Method)
In This Method The Measure Is Represented By A Fraction. The Fraction Shown Represents The Distance Measured On The Map And On The Ground. In This Fraction The Numerator’s Value Is Always 1 While The Denominator’s Value Varies According To The Measure.
In Denominator Fractions, The Numerator And Denominator Are Always Expressed In The Same Unit. Representative Fraction (RF) = Distance On Map/Distance On Surface Geography And Experimental Geography Of India For Example, If The Representational Fraction Of A Map Is 1 : 40,000, It Would Mean That The Distance Between The Map And The Surface Is In The Ratio Of 1 To 40,000. Whether The Distance Is In Inches Or Cm. Be In
Like 1 Cm. : 40,000 Cm. Would Mean 1 Cm On The Map. At A Distance Of 40,000 Cm On The Ground. Will Represent The Distance. Like The Normal Statement Method, In This Method Also The Scale Shown Becomes Inaccurate When The Size Of The Map Is Changed.
(3) Linear Measurement Method ( Linear Scale Methed )
In This Method, The Measure Is Represented By A Straight Line Whose Length Represents The Actual Distance Taken On The Ground In A Certain Proportion. Then This Straight Line Is Divided Into Primary And Secondary Parts And On Those Parts The Values Of The Actual Distances To The Surface Are Marked.
The Specialty Of This Method Is That Even After Changing The Size Of The Map, The Scale Shown Remains Pure Because The Size Of The Scale Becomes Bigger Or Smaller In Proportion To The Size Of The Map.
Conversion Of Rulers ( Conversion Of Scales )
(1) Converting Or Converting An Ordinary Statement Measure Into A Denominator Fraction
Example: The General Statement Of A Map Is The Measure 1 Cm : 10 Km Find Its Representative Fraction. Given Simple Statement: Measurement = 1 Cm : 10 Km I.E. Distance On The Map 1 Cm = Distance On The Ground 10 Km
We Know That The Denominator Fraction = Distance On The Map Distance On The Ground
Ie RE = 1 Cm / 10 Km
Because Numerator And Denominator Are Expressed In The Same Unit In The Demonstrative Fraction, So Here Km. To Cm. Will Have To Be Converted Into
We Know That 1 Km = 1,00,000 Cm
So RE=
Since No Measurement System Is Used In The Denominator Fraction, Therefore
Representative Fraction (RE)= 1/10000 Or 1 : 10,00,000
(2) Converting Or Converting A Demonstrative Fraction Into An Ordinary Statement Measure
Example: A Demonstrative Fraction Is 1 : 633600, Then Convert It To A Simple Statement Measure To Represent It In Miles. Given Display Fraction = 1:633600 Because Here The Display Fraction Has To Be Converted Into Miles So The Given Display Fraction Has To Be Considered In Inches I.E. 1 Inch : 633600 Inch Which Means
1 Inch Distance On The Map Represents 633600 Inch Distance Of The Ground.
Action – 1 Inch : 633600
Inches Here We Have To Convert Inches To Miles.
We Know 1 Mile = 63360 Inches
Scale = 1 Inch :- 633600 / 63360 Mile
Or 1 Inch: 10 Miles
So The Simple Statement Measure = 1 Inch : 10 Miles
Division Of A Straight Line Into Equal Parts
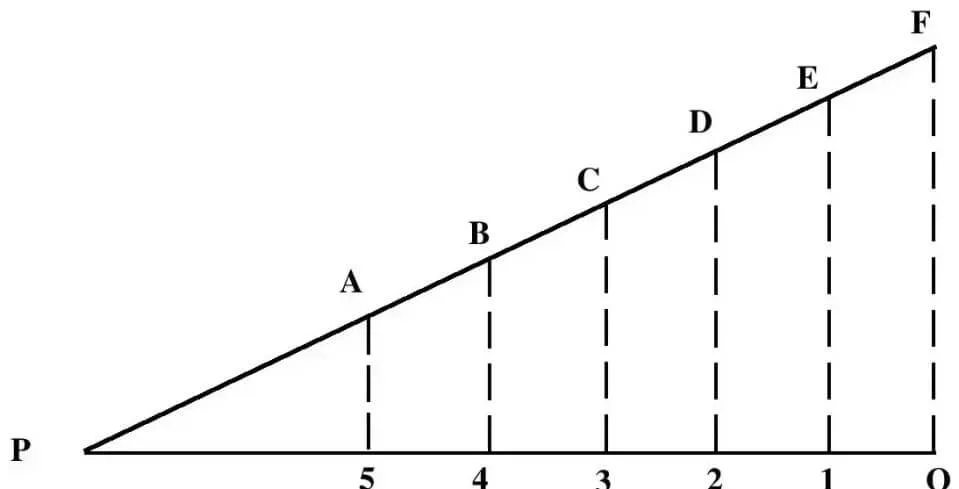
To Make A Linear Measure, It Is Necessary To First Divide The Straight Line Shown Into Equal Parts. There Are Two Geometric Methods Of Dividing A Straight Line Into Equal Parts.
First Method Suppose A Straight Line PQ Is Given Which Has To Be Divided Into 6 Equal Parts. First Of All Draw A Straight Line At Point P Making An Acute Angle With The Help Of Compasses. Then Mark 6 Points A, B, C, D, E, F At Equal Distance On This Line With The Help Of Compass From Point P.
Join The Point F With The Point Q. Then With The Help Of Set-Square Draw Lines E-1, D-2, C-3, B-4 And A-5 From Points A, B, C, D And E Parallel To The FQ Line Which Will Intersect The PQ Line With P-5. , 5-4, 4-3, 3-2, 2-1 And 1Q,6 Will Divide Into Equal Parts.
Second Method Let Us Assume A Straight Line PQ Is Given. Which Is To Be Divided Into 6 Equal Parts, First Take A Straight Line PQ, Then Draw Two Equal Acute Angles From The Point P Upwards And Downwards From The Point Q. Mark A, B, C, D, E, F And G, H, IJ, K, L At Equal Distances On These Two Lines With The Help Of Compasses.
Now Join F With Q, E With G, D With I, B With J, A With K And P With L In Such A Way That They Line QR As 1, 2, 3, 4, Cut At 5. Thus P-5, 5-4, 4-3, 3-2, 2-1 And LQ Will Be 6 Equal Parts Of The PQ Line.
Rulers Of Class ( Categories Of Scales )
On The Basis Of Construction Method And Purposes, Scales Are Kept In 5 Classes.
1. Large Scale
2. Small Scale
3. Simple Scale
4. Diagonal Scale
5. Comparative Scale
(1) Large Scale ( Large Scale ) –
The Scale By Which The Smaller Distances On The Surface Are Represented By The Longer Distances On The Map Is Called The Larger Scale, That Is, The Scale Whose Representative Fraction (RE) Is Larger Is The Larger Scale.
For Example 20 Cm : 1 Km (RE 1 : 5,000) Which Means 20 Cm Long Line On The Map Shows Only 1 Km Distance On The Ground. The Maps Made By This Scale Provide Detailed Information Of The Area Shown. In These, Secondary Symptoms Are Also Displayed. Real Estate Maps And Topographic Maps, Being Built On A Large Scale, Provide Detailed Information.
(2) Small Scale ( Small Scale ) –
The Scale By Which Long Distances On The Ground Are Shown By Small Distances On The Map Is Called Small Scale. The Representing Fraction (R..) Of The Smaller Scale Is Also Smaller. For Example: 1 Cm: 20 Km Which Means 1 Cm Long Line On The Map Shows The Distance Of 20 Km On The Ground.
Maps Made On A Small Scale Show The Vast Area, But It Is Not Possible To Show Secondary Features In These Maps. Atlas And Walls, Maps Are Made In Them On A Small Scale.
(3) Simple Ruler ( Plain Scale ) –
As The Name Suggests, This Scale Is Very Easy To Make. This Scale Is Represented By A Straight Line Whose Length Is Between 5 To 8 Inches Or 12 To 20 Cm. First Of All, This Line Is Divided Into Equal Primary Divisions According To The Need, Which Show The Long Distances Of The Surface.
After This, To Read Small Distances, The First Primary Part On The Left Side Of The Scale Is Divided Into Equal Secondary Divisions Which Represent Small Distances On The Surface. Surface Distances Are Marked On The Primary And Secondary Parts Of The Line. Zero Is Always Marked Except For The Primary Part On The Left.
The Surface Distances Marked On The Scale Should Be In Round Figures. The Simple Statement Must Be Written With A Simple Scale, The Measure Or The Denominator Fraction. This Scale Is Also Known As Linear Scale Or Graphic Scale.
Example : The Representation Fraction Of A Map Is 1 : 20,00,000 Construct A Simple Scale To Read Distance In Kilometers. Formation Method- Given Representative Fraction (RE) = 1 : 20,00,000 I.E. 1 Cm Long Line On The Map Represents 20,00,000 Cm Long Line On The Surface.
Let A Straight Line 15 Cm Be Taken To Make The Scale, Which Is Equal To The Surface Area According To The Given Representational Fraction.
20,00,000 / 100000 X 15 = 300 Km.
Scale
First Of All Take A Straight Line 15 Cm Long And Do 5 Equal Primary Parts Of It. Each Primary Part Will Represent A Distance Of 60 Km From The Ground. Then The First Primary Part On The Left Is Divided Into 5 Equal Secondary Parts, Each Part Will Represent 12 Km Distance Of The Ground.

Mark Zero Except The First Primary Part. From Zero To The Right Mark 60, 120, 180 And 240 On The Primary Parts Respectively And From Zero To The Left And Minor Parts Mark 12, 24, 36, 48 And 60 Respectively At Both Ends Of The Scale. Write Down The Kilometer. Write The Representative Fraction (RF) Given Above The Scale, In This Way A Simple Scale Will Be Ready.
(4) Diagonal Ruler ( Diagonal Scale )
The Scale In Which The Minor Parts Are Divided Into Smaller Parts By Using Diagonals Is Called Diagonal Scale. In Simple Scale Only Two Units Like Mile-Long, Kilometer, Hectometer Etc. Can Be Read While In Diagonal Scale Distances Can Be Read In Three Units Like Mile-Phalang-Yard Or Kilometer-Hectometer-Decameter. The Construction Method Of Making The First Two Units In The Diagonal Scale Is According To The Simple Scale, While The Distance Of The Third Unit Is Made By Drawing The Diagonals In The Rectangles Made On The Secondary Side Of The Scale.
For Example – Suppose The Number Of Parallel Lines Drawn At Equal Spacing In Addition To The Horizontal Line In A Rectangle Is 5, Then The Diagonal Of The Rectangle Divides The First Line Into 1 : 4, The Second 2 : 3, The Third 3 : 2, The Fourth In 4 : 1. Will Divide. And The Fifth Side Will Represent The Length Of The Horizontal Side Of The Rectangle. Suppose The Length Of The Secondary Part (Horizontal Side) Is 1 Cm, Then The Distances Of 0.2, 0.4, 0.6, 0.8 Cm Can Be Easily Read On The Lines Drawn At Equal Spacing Respectively. The Last Ie The Fifth Line Will Not Be Divided By The Diagonal, So Its Value Is 1 Cm And
Will Be 1 Cm. The Special Thing Here Is That Equal Number Of Straight Lines Are Drawn Parallel To The Horizontal Side Of The Rectangle To Divide The Secondary Part Into As Many Parts.
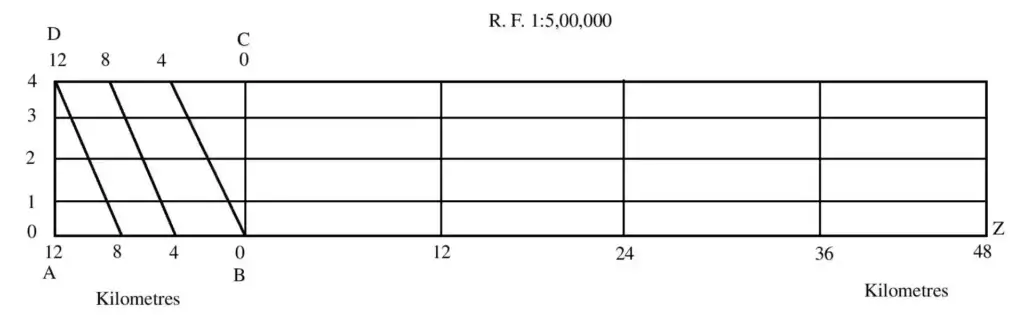
Example : The Representative Fraction Of A Map Is 1 : 5,00,000.
For This, Make A Diagonal Measure In Which The Distance Up To 1 Km Can Be Read.
Formation Method – Given Representative Fraction = 1 : 5,00,000
That Is, 1 Cm On The Map = 5,00,000 Cm On The Ground Or 1 Cm = 5 Km
12 Cm Long Line Will Show Distance = 5 X 12 = 60 Km
First Take A Straight Line AZ 12 Cm Long. Divide It Into 5 Equal Primary Parts, Each Part Will Represent A Distance Of 12 Km, Then Divide The First Primary Part AB On The Left Into 3 Equal Secondary Parts. Each Minor Part Will Represent A Distance Of 4 Km. Write Its Value On Each Primary And Secondary Part. Each
1c.M. Draw Perpendicular To The Primary Part. Cut 4 Equal Parts At Equal Distances On The Perpendicular AD To The Left And From Those Parts Draw Lines Parallel To The Line AZ. Divide The Side CD Of The Rectangle ABCD On The Left And The Primary Side Like AB Into 3 Equal Geography Minor Parts. And Mark Their Values. Now Draw A Diagonal Joining The 4 Km Point Of Side CD With The 0 Km Point Of AB, The 8 Km Point With The 4 Km Point And The 12 Km Point With The 8 Km Point. Thus The Diagonal Scale Will Be Ready.
5) Comparative Ruler ( Comparative Scale )
The Scale By Which Distances Can Be Displayed In More Than One Measurement System Is Called Comparative Scale. Like Miles And Kilometers, Meters And Yards Etc. Sometimes A Comparative Display Of Time And Distance Is Also Done By This Scale.
Features Of Comparative Scale
1. Comparative Scales Are Made On The Same Representative Fraction.
2. The Zero Point Of Comparative Scales Is Always In A Vertical Straight Line. Sometimes The Comparative Scales Are Not Separated And The Same Simple Scale Is Divided In Such A Way That The Same Part Of The Scale Can Easily Show Two Different Measurements.
Example- Construct A Comparative Scale For A Map To Show Distances In Kilometers And Miles. Which Represents The Fraction From 1 : 6,33,600.
Action – Km. For Scale: According To The Given Example, A 1 Cm Long Line On The Map Represents A Distance Of 6,33,600 Cm From The Ground.
Or A 15 Cm Long Line On The Map Will Show =95.04 Km On The Ground.
But 95.04 Is Not A Whole Number So We Take 100 Km As A Whole Number.
100 Km Distance On The Map
100/95.04 X 15 = 15.8 Cm Long Line.
First Take A Straight Line 15.8 Cm Long, Divide It Into 5 Equal Primary Parts, Each Part Will Represent 20 Km Distance Of The Ground. Then Divide The First Primary Part On The Left Into 5 Equal Secondary Parts, Each Part Will Represent 4 Km Distance Of The Ground. Write The Km On Both The Ends Of The Scale. Mark The Value Of Each Part Action- Given To Measure Miles